Modules
	Linear Algebra

	Optimisation
	This module contains optimisation methods for Newton type optimisation.

Classes
class	go3Vector< T >
	3-dimensional vector. More...

class	goBiorthoWavelet

class	goComplex< T >
	Complex number class. More...

class	goMath::CubicSpline< T >
	Cubic interpolating splines. More...

class	goMath::CubicSplineND< T >
	Cubic interpolating splines. More...

class	goCurve< T >
	Curve representation. More...

class	goSignal::TVL1
	TV-regularised L1-norm approximation of an image after [1]. More...

class	goMath::GaussPDF< input_type, output_type >
	Gauss' probability density function. More...

class	goMath::MultiGaussPDF< input_vector, scalar_type >
	Vector values Gauss distribution. More...

class	goMath::Manifold< element_type, tangent_type >
	Interface for manifolds. More...

class	goMath::SO3< T >
	Rotation group. More...

class	goMath::LinearSpace< T >
	Simple linear vector space. More...

class	goMath::UnitSphere< T >
	Unit sphere. More...

class	goMath::PDF< input_type, output_type >
	Probability density function base template. More...

class	goPointCloud< T >
	Point cloud. More...

class	goQuaternion< T >
	Quaternion class. More...

class	goSparseMatrix
	Basic sparse matrix class with Matlab mxArray support. More...

class	goMath::ThinSVD< Real >

Typedefs
typedef go4Vector< goFloat >	go4Vectorf
	4-dimensional vector. More...

typedef go4Vector< goDouble >	go4Vectord

typedef goCurve< goFloat >	goCurvef

typedef goCurve< goDouble >	goCurved

typedef goPointCloud< goFloat >	goPointCloudf

Enumerations
enum	{ UNSORTED, ROW_WISE, COLUMN_WISE }

Functions
template<class iterator_type , class manifold_type >
bool	goMath::karcherMean (iterator_type start, int count, manifold_type &manifold, typename manifold_type::Element &meanRet, int max_iterations=1000, double epsilon=1e-6)
	Karcher mean for generic Riemannian manifolds. More...

template<class T >
T	goMath::mod (T value, T modulus)
	Modulus function. More...

template<class Real >
Real	goMath::abs (Real a)

template<class Real >
Real	goMath::hypot (const Real &a, const Real &b)

template<class Real >
Real	goMath::acos (const Real &a)

template<class Scalar >
Scalar	goMath::min (Scalar a, Scalar b)

template<class Scalar >
Scalar	goMath::max (Scalar a, Scalar b)

template<class T >
T	goMath::max (const goFixedArray< T > &a)

template<class T >
goSize_t	goMath::maxIndex (const goFixedArray< T > &a)

template<class T >
T	goMath::min (const goFixedArray< T > &a)

template<class T >
goSize_t	goMath::minIndex (const goFixedArray< T > &a)

template<class T >
T	goMath::maxabs (const goFixedArray< T > &a)

template<class T >
T	goMath::minabs (const goFixedArray< T > &a)

	goSparseMatrix::goSparseMatrix (int rows=0, int cols=0)

void	goSparseMatrix::init ()

void	goSparseMatrix::setSize (int rows, int cols)

void	goSparseMatrix::set (int row, int col, double value)
	Not implemented. More...

int	goSparseMatrix::getElementCount () const
	Get the total number of nonzero elements. More...

int	goSparseMatrix::getSortType () const

bool	goSparseMatrix::fillBegin (int elementCount)
	Begin filling elementCount elements in this matrix. More...

int	goSparseMatrix::fillNext (int row, int col, double value)
	Fills the next element in this matrix. More...

void	goSparseMatrix::fillEnd (int sortType=ROW_WISE)
	Ends filling the matrix. More...

bool	goSparseMatrix::matrixVectorMult (goArray< goDouble > &ret, const goArray< goDouble > &v)
	(this) * v More...

template<class Tv >
bool	goSparseMatrix::matrixVectorMult (goMath::Vector< Tv > &ret, const goMath::Vector< Tv > &v)
	(this) * v More...

bool	goSparseMatrix::vectorMatrixMult (goArray< goDouble > &ret, const goArray< goDouble > &v)
	v' * (this) More...

bool	goSparseMatrix::matrixVectorMult (goSparseMatrix &ret, const goArray< goDouble > &v)
	(this) * v More...

template<class Tv >
bool	goSparseMatrix::matrixVectorMult (goSparseMatrix &ret, const goMath::Vector< Tv > &v)
	(this) * v More...

bool	goSparseMatrix::vectorMatrixMult (goSparseMatrix &ret, const goArray< goDouble > &v)
	v' * (this) More...

bool	goSparseMatrix::matrixMatrixMult (goSparseMatrix &ret, goSparseMatrix &m)

bool	goSparseMatrix::matrixMatrixAdd (goSparseMatrix &ret, goSparseMatrix &m)

bool	goSparseMatrix::matrixMatrixSubtract (goSparseMatrix &ret, goSparseMatrix &m)

goSparseMatrix &	*goSparseMatrix::operator=** (goDouble scalar)

goSparseMatrix	goSparseMatrix::operator* (const goSparseMatrix &other) const

template<class Tv >
goMath::Vector< Tv >	goSparseMatrix::operator* (const goMath::Vector< Tv > &v) const

goSparseMatrix	goSparseMatrix::operator* (goDouble s) const

goSparseMatrix	goSparseMatrix::operator+ (const goSparseMatrix &m) const

goSparseMatrix	goSparseMatrix::operator- (const goSparseMatrix &m) const

goIndex_t	goSparseMatrix::row (goIndex_t elementIndex) const
	Returns the row of the element at elementIndex.

goIndex_t	goSparseMatrix::column (goIndex_t elementIndex) const
	Returns the row of the element at elementIndex.

goDouble	goSparseMatrix::value (goIndex_t elementIndex) const
	Returns the value of the element at elementIndex.

int	goSparseMatrix::getRowCount () const
	Returns the number of rows.

int	goSparseMatrix::getColumnCount () const
	Returns the number of columns.

const goArray< goIndex_t > &	goSparseMatrix::getRowStart () const
	For row-sorted matrices.

const goArray< goIndex_t > &	goSparseMatrix::getColStart () const
	For column-sorted matrices.

void	goSparseMatrix::sortRows (bool sort_columns=false)
	Sorts in ascending row order. More...

void	goSparseMatrix::sortColumns (bool sort_rows=false)
	Sorts in ascending column order. More...

void	goSparseMatrix::findRows ()

void	goSparseMatrix::findColumns ()

bool	goSparseMatrix::appendRow (const goSparseMatrix &r)
	Appends the row matrix r to this matrix. More...

bool	goSparseMatrix::appendRows (const goSparseMatrix &m)

void	goSparseMatrix::transpose ()

goArray< goIndex_t > &	goSparseMatrix::getColIndex ()

const goArray< goIndex_t > &	goSparseMatrix::getColIndex () const

goArray< goIndex_t > &	goSparseMatrix::getRowIndex ()

const goArray< goIndex_t > &	goSparseMatrix::getRowIndex () const

goArray< goDouble > &	goSparseMatrix::getValues ()

const goArray< goDouble > &	goSparseMatrix::getValues () const

void	goSparseMatrix::setSortType (int t)

template<class T >
bool	goMath::euclideanToBarycentric (const goMath::Matrix< T > &simplex, const goMath::Vector< T > &point, goMath::Vector< T > &ret)
	Convert euclidean to barycentric coordinates. More...

template<class MatrixType , class VectorType >
goDouble	goMath::goConjugateGradients (const MatrixType &A, const VectorType &b, VectorType &x, goDouble epsilon=1e-6)
	Conjugate gradients solver. More...

template<class T >
bool	goMath::resampleCubic (const goMath::Matrix< T > &source, goMath::Matrix< T > &target, goSize_t resamplePointCount, bool closed=false, goFixedArray< goDouble > *accumLength_=0)
	Piecewise cubic resampling of a curve represented by a configuration matrix. More...

template<class T >
void	goMath::resampleLinear (const goFixedArray< T > &f, goFixedArray< T > &ret)

bool	goMath::laplacian2D (const goSignal3DBase< void > &sig, goSignal3DBase< void > &retValue)
	Calculates the laplacian (2nd derivative) of a 2D signal (z-size == 1). More...

bool	goMath::gradient2D (const goSignal3DBase< void > &sig, goSignal3DBase< void > &retValue)
	Calculates the gradient of a 2D signal (z-size == 1). More...

bool	goMath::ddx2D (const goSignal3DBase< void > &sig, goSignal3DBase< void > &retValue)
	Calculates the derivative in x direction assuming a 2D signal. More...

bool	goMath::ddy2D (const goSignal3DBase< void > &sig, goSignal3DBase< void > &retValue)
	Calculates the derivative in y direction assuming a 2D signal. More...

bool	goMath::centralDifferences (const goSignal3DBase< void > &x, goSignal3DBase< void > &retValue, int dimension=0, goDouble h=1.0, const goSignal3DBase< void > *mask=0)
	Calculate central finite differences in a given direction. More...

bool	goMath::forwardDifferences (const goSignal3DBase< void > &x, goSignal3DBase< void > &retValue, int dimension=0, goDouble h=1.0, const goSignal3DBase< void > *mask=0)
	Calculate forward finite differences in a given direction. More...

bool	goMath::backwardDifferences (const goSignal3DBase< void > &x, goSignal3DBase< void > &retValue, int dimension=0, goDouble h=1.0, const goSignal3DBase< void > *mask=0)
	Calculate backward finite differences in a given direction. More...

bool	goMath::curvatureDirect2D (const goSignal3DBase< void > &input, goSignal3D< void > &result, goDouble hx=1.0, goDouble hy=1.0)

template<class T >
T	goMath::integrate (const goMath::Vector< T > &v)
	Sehnentrapezformel. Step width (h) is assumed 1, so normalisation may be needed afterwards. More...

template<class T >
T	goMath::integrateSimpson (const goMath::Vector< T > &v)
	Integration with Simpson rule. Step width h is assumed 1, so normalisation may be needed afterwards. More...

template<class T >
T	goMath::integrateSum (const goMath::Vector< T > &v)

template<class T >
T	goMath::stencil (const goSignal3DBase< void > &sig, const goMath::Matrix< T > &s)
	Calculate 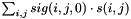$\sum_{i,j} sig(i,j,0) \cdot s(i,j)$ . More...

void	goMath::transform2D (const goSignal3DBase< void > &source, goDouble scale, goDouble angle, goDouble t_x, goDouble t_y, goSignal3D< void > &target, bool setsize=true)
	2D euclidean transformation of an image. More...

void	goMath::scale2D (const goSignal3DBase< void > &source, goSignal3DBase< void > &target, bool keep_aspect=false)
	Scale `source` into `target`. More...

void	goMath::paste2D (const goSignal3DBase< void > &source, goDouble scale, goDouble angle, goDouble t_x, goDouble t_y, goSignal3DBase< void > &target, goFloat bgColour)
	Paste `source` at under some euclidean transformations into `target`. More...

Detailed Description

Typedef Documentation

◆ go4Vectorf

typedef go4Vector<goFloat> go4Vectorf

4-dimensional vector.

Todo:: make this a descendant of goMath::Vector, fix size to 4, provide x,y,z,t/w as references.

Function Documentation

◆ abs()

template<class Real >

Real goMath::abs ( Real a )

Returns: the absolute value of a real (no-complex) scalar.

◆ acos()

template<class Real >

Real goMath::acos ( const Real & a )

::acos seems to result in nan when the argument is exactly 1.0 (contrary to the manpage!). That is caught here.

Returns: acos (a)

◆ appendRow()

bool goSparseMatrix::appendRow ( const goSparseMatrix & r )

inline

Appends the row matrix r to this matrix.

The result is [(*this)' r']'

Parameters

r	Must be of size (1, this->getColumnCount())

Returns: True if successful, false otherwise.

◆ appendRows()

bool goSparseMatrix::appendRows ( const goSparseMatrix & m )

inline

Bug:: After appending rows, findRows() should be called when this matrix is row-sorted. This needs to be fixed or it will lead to misunderstandings and malfunctioning code/hard to find errors.

◆ backwardDifferences()

bool goMath::backwardDifferences	(	const goSignal3DBase< void > &	x,
		goSignal3DBase< void > &	retValue,
		int	dimension = `0`,
		goDouble	h = `1.0`,
		const goSignal3DBase< void > *	mask = `0`
	)

Calculate backward finite differences in a given direction.

Parameters

x	Data grid.
retValue	Contains finite differences after the function returns true. If the size of retValue does not match the size of x and retValue is a goSignal3D<void>, retValue will be resized to the size of x, including number of channels, blocksize of x and border of 1 in each direction.
dimension	Dimension (0, 1, or 2 for x, y, or z)
h	Grid spacing (default 1)
mask	Optional mask of type goInt8. If given, central differences are only calculated where mask is != 0. The other values in retValue are not changed. Default: NULL.

Note: Only goFloat and goDouble data are supported. The data types of x and retValue may differ. Both are given by the user, so the data type of retValue must be set before calling this function. It may be of wrong size, in which case it must point to a goSignal3D<void> in order for it to be resizable.; The algorithm is run for all channels.

Returns: True if successful, false otherwise.

Author: Christian Gosch

◆ centralDifferences()

bool goMath::centralDifferences	(	const goSignal3DBase< void > &	x,
		goSignal3DBase< void > &	retValue,
		int	dimension = `0`,
		goDouble	h = `1.0`,
		const goSignal3DBase< void > *	mask = `0`
	)

Calculate central finite differences in a given direction.

Parameters

x	Data grid.
retValue	Contains finite differences after the function returns true. If the size of retValue does not match the size of x and retValue is a goSignal3D<void>, retValue will be resized to the size of x, including number of channels, blocksize of x and border of 1 in each direction.
dimension	Dimension (0, 1, or 2 for x, y, or z)
h	Grid spacing (default 1)
mask	Optional mask of type goInt8. If given, central differences are only calculated where mask is != 0. The other values in retValue are not changed. Default: NULL.

Note: Only goFloat and goDouble data are supported. The data types of x and retValue may differ. Both are given by the user, so the data type of retValue must be set before calling this function.; The algorithm is run for all channels.

Returns: True if successful, false otherwise.

Author: Christian Gosch

◆ ddx2D()

bool goMath::ddx2D	(	const goSignal3DBase< void > &	sig,
		goSignal3DBase< void > &	retValue
	)

Calculates the derivative in x direction assuming a 2D signal.

This function calculates the derivative in x-direction while assuming the signal is 2-dimensional. The arguments are restricted to signals of type GO_FLOAT and GO_DOUBLE.

Todo:: Implement for 3D-signals.

Parameters

sig	Signal to calculate the derivative of.
retValue	After the function returned true, contains the x-derivative of sig. Must be of the same size as sig.

Returns

◆ ddy2D()

bool goMath::ddy2D	(	const goSignal3DBase< void > &	sig,
		goSignal3DBase< void > &	retValue
	)

Calculates the derivative in y direction assuming a 2D signal.

This function calculates the derivative in y-direction while assuming the signal is 2-dimensional. The arguments are restricted to signals of type GO_FLOAT and GO_DOUBLE.

Todo:: Implement for 3D-signals.

Parameters

sig	Signal to calculate the derivative of.
retValue	After the function returned true, contains the y-derivative of sig. Must be of the same size as sig.

Returns

◆ euclideanToBarycentric()

template<class T >

bool goMath::euclideanToBarycentric	(	const goMath::Matrix< T > &	simplex,
		const goMath::Vector< T > &	point,
		goMath::Vector< T > &	ret
	)

Convert euclidean to barycentric coordinates.

This works only for vertices with n+1 points in n dimensions.

Parameters

simplex	Simplex points, one point per column
point	Point in euclidean coordinates
ret	On return, contains barycentric coordinates of point.

Returns: True if successful, false otherwise (also check log).

◆ fillBegin()

bool goSparseMatrix::fillBegin ( int elementCount )

inline

Begin filling elementCount elements in this matrix.

The actual amount of elements filled in can be lower than elementCount. Do not forget to call fillEnd() when done filling in values.

Parameters

elementCount Maximum number of elements to be filled in.

Returns: True if successful, false otherwise.

◆ fillEnd()

void goSparseMatrix::fillEnd ( int sortMethod = ROW_WISE )

inline

Ends filling the matrix.

Ends filling and resizes the internal arrays according to the number of elements filled in.

◆ fillNext()

int goSparseMatrix::fillNext	(	int	row,
		int	col,
		double	value
	)

inline

Fills the next element in this matrix.

Parameters

row	Row of the element
col	Column of the element
value	Value of the element

Returns: Number of elements that can still be filled in after this call. If zero, all subsequent calls to fillNext() will not change the matrix.

◆ forwardDifferences()

bool goMath::forwardDifferences	(	const goSignal3DBase< void > &	x,
		goSignal3DBase< void > &	retValue,
		int	dimension = `0`,
		goDouble	h = `1.0`,
		const goSignal3DBase< void > *	mask = `0`
	)

Calculate forward finite differences in a given direction.

Parameters

x	Data grid.
retValue	Contains finite differences after the function returns true. If the size of retValue does not match the size of x and retValue is a goSignal3D<void>, retValue will be resized to the size of x, including number of channels, blocksize of x and border of 1 in each direction.
dimension	Dimension (0, 1, or 2 for x, y, or z)
h	Grid spacing (default 1)
mask	Optional mask of type goInt8. If given, central differences are only calculated where mask is != 0. The other values in retValue are not changed. Default: NULL.

Note: Only goFloat and goDouble data are supported. The data types of x and retValue may differ. Both are given by the user, so the data type of retValue must be set before calling this function. It may be of wrong size, in which case it must point to a goSignal3D<void> in order for it to be resizable.; The algorithm is run for all channels.

Returns: True if successful, false otherwise.

Author: Christian Gosch

◆ getElementCount()

int goSparseMatrix::getElementCount ( ) const

inline

Get the total number of nonzero elements.

nnz() in Matlab.

Returns: Number of nonzero elements.

◆ goConjugateGradients()

template<class MatrixType , class VectorType >

goDouble goMath::goConjugateGradients	(	const MatrixType &	A,
		const VectorType &	b,
		VectorType &	x,
		goDouble	epsilon = `1e-6`
	)

Conjugate gradients solver.

Conjugate gradients method for solving linear equation systems.

Solves A*x=b iteratively for x.

Note: Currently implemented for goSparseMatrix and goMath::Vector.

Parameters

A	Matrix A
b	Vector b
x	Solution
epsilon	Stop when abs(Ax-b) < epsilon.

Returns: final abs(A*x-b).

Finde einen Vektor x fuer A*x=b. Geht momentan nur fuer goSparseMatrix.

Todo:: Spezialimplementierung fuer goSparseMatrix (gibts schon) und Standardimplementierung fuer andere Matrizen.

Parameters

A	Matrix A
b	Vector b
x	Solution x
epsilon	Error bound.

Returns: Error.

◆ gradient2D()

bool goMath::gradient2D	(	const goSignal3DBase< void > &	sig,
		goSignal3DBase< void > &	retValue
	)

Calculates the gradient of a 2D signal (z-size == 1).

Note: The data type of the arguments is currently restricted to GO_FLOAT and GO_DOUBLE.

Todo:: Look at the code and find the reference where this is documented. It's not simply central differences, but rather central differences including the next neighbours.

Parameters

sig	Contains the 2D signal.
retValue	After returning true, retValue contains the x and y components of grad(sig). retValue must be of the same size as sig in x and y dimensions and its channel-count must be 2.

Returns: True if successful, false otherwise.

◆ hypot()

template<class Real >

Real goMath::hypot	(	const Real &	a,
		const Real &	b
	)

Returns: hypotenuse of real (non-complex) scalars a and b by avoiding underflow/overflow using (a * sqrt( 1 + (b/a) * (b/a))), rather than sqrt(a*a + b*b).

◆ integrate()

template<class T >

T goMath::integrate ( const goMath::Vector< T > & v )

Sehnentrapezformel. Step width (h) is assumed 1, so normalisation may be needed afterwards.

Parameters

v	Vector with function values at equidistant points.

Returns: Integral approximation.

◆ integrateSimpson()

template<class T >

T goMath::integrateSimpson ( const goMath::Vector< T > & v )

Integration with Simpson rule. Step width h is assumed 1, so normalisation may be needed afterwards.

The composite Simpson rule is 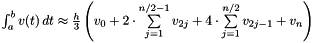$\int_a^b v(t) \, dt \approx \frac{h}{3} \left( v_0 + 2 \cdot \sum\limits_{j=1}^{n/2-1} v_{2j} + 4 \cdot \sum\limits_{j=1}^{n/2} v_{2j-1} + v_n\right)$ , if the continuous function v(t) is divided into an even number n of equidistant intervals with distance h. Note that integrateSimpson samples linearly between points given in v to obtain an even number of sampled points. Also, only the division by 6 (not 3!) is done, since the step width h is assumed to be one. Normalisation may therefore be done after calling this function by the user, e.g. if the interval [a,b] has length one, by multiplying with 1/v.getSize().

Parameters

v	Vector with function values at equidistant points.

Returns: Integral approximation.

◆ karcherMean()

template<class iterator_type , class manifold_type >

bool goMath::karcherMean	(	iterator_type	start,
		int	count,
		manifold_type &	manifold,
		typename manifold_type::Element &	meanRet,
		int	max_iterations = `1000`,
		double	epsilon = `1e-6`
	)

Karcher mean for generic Riemannian manifolds.

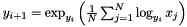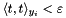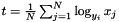The Karcher mean is calculated by iterating using the update step $y_{i+1} = \exp_{y_i} \left( \frac{1}{N} \sum_{j=1}^N \log_{y_i} x_j \right)$ until max_iterations has been reached or until $\langle t,t \rangle_{y_i} < \varepsilon$ , with $t = \frac{1}{N} \sum_{j=1}^N \log_{y_i} x_j$ .

Parameters

start	Start iterator, pointing to the first element x_j.
count	Number of elements N.
manifold	Manifold object (e.g. SO3).
meanRet	Return value, contains the mean after returning true.
max_iterations	Max. number of iterations. Default: 1000
epsilon	"Small" floating point value. Default: 1e-6

Returns: True if mean could be found within max_iterations, false otherwise.

Examples: karchermean/km.cpp.

◆ laplacian2D()

bool goMath::laplacian2D	(	const goSignal3DBase< void > &	sig,
		goSignal3DBase< void > &	retValue
	)

Calculates the laplacian (2nd derivative) of a 2D signal (z-size == 1).

Note: The data type of the arguments is currently restricted to GO_FLOAT, but GO_DOUBLE will also be implemented. Multichannel data is not yet supported by libGo.

Parameters

sig	Contains the 2D signal.
retValue	After returning true, retValue contains the laplace(sig). retValue must be of the same size as sig in x and y dimensions and its z dimension must be 1.

Todo:: BUG: This sometimes can produce NaNs.

Returns: True if successful, false otherwise.

◆ matrixVectorMult() [1/4]

bool goSparseMatrix::matrixVectorMult	(	goArray< goDouble > &	ret,
		const goArray< goDouble > &	v
	)

inline

(this) * v

Parameters

ret
v

Returns

◆ matrixVectorMult() [2/4]

template<class Tv >

bool goSparseMatrix::matrixVectorMult	(	goMath::Vector< Tv > &	ret,
		const goMath::Vector< Tv > &	v
	)

inline

(this) * v

Parameters

ret
v

Returns

◆ matrixVectorMult() [3/4]

bool goSparseMatrix::matrixVectorMult	(	goSparseMatrix &	ret,
		const goArray< goDouble > &	v
	)

inline

(this) * v

Parameters

ret
v

Returns

◆ matrixVectorMult() [4/4]

template<class Tv >

bool goSparseMatrix::matrixVectorMult	(	goSparseMatrix &	ret,
		const goMath::Vector< Tv > &	v
	)

inline

(this) * v

Parameters

ret
v

Returns

◆ max()

template<class Scalar >

Scalar goMath::max	(	Scalar	a,
		Scalar	b
	)

Returns: the maximum of scalars a and b.

◆ min()

template<class Scalar >

Scalar goMath::min	(	Scalar	a,
		Scalar	b
	)

Returns: the minimum of scalars a and b.

◆ mod()

template<class T >

T goMath::mod	(	T	value,
		T	modulus
	)

Modulus function.

Parameters

value
modulus

Returns: value mod modulus

◆ paste2D()

void goMath::paste2D	(	const goSignal3DBase< void > &	source,
		goDouble	scale,
		goDouble	angle,
		goDouble	t_x,
		goDouble	t_y,
		goSignal3DBase< void > &	target,
		goFloat	bgColour
	)

Paste source at under some euclidean transformations into target.

Parameters

source	Source patch
scale	scale factor
angle	rotation angle
t_x	Translation x
t_y	Translation y
target	target signal (is left unchanged except for the pasted `source`)
bgColour	Transparent colour in `source`. Only points which have different colour values are pasted into `target`.

◆ resampleCubic()

template<class T >

bool goMath::resampleCubic	(	const goMath::Matrix< T > &	source,
		goMath::Matrix< T > &	target,
		goSize_t	resamplePointCount,
		bool	closed = `false`,
		goFixedArray< goDouble > *	accumLength_ = `0`
	)

Piecewise cubic resampling of a curve represented by a configuration matrix.

The source matrix contains a point in each row, so does the target matrix after successful completion of the function.

Parameters

source	Source points.
target	Target points.
resamplePointCount	Point count intended for target.
closed	If true, the source points will be treated as a closed curve, i.e. the first and last points are connected.

Returns: True if successful, false otherwise.

◆ scale2D()

void goMath::scale2D	(	const goSignal3DBase< void > &	source,
		goSignal3DBase< void > &	target,
		bool	keep_aspect = `false`
	)

Scale source into target.

Todo:: Extend to 3D – this only requires to write a 3D sampling function.

Parameters

source	Original 2D signal
target	Target 2D signal
keep_aspect	If true, keep aspect ratio

◆ set()

void goSparseMatrix::set	(	int	row,
		int	col,
		double	v
	)

inline

Not implemented.

A general set function would require some reallocating and copying of arrays. I had no use for that so far, but please implement it AND GIVE IT BACK TO ME if you need it.

Parameters

row
col
v

◆ sortColumns()

void goSparseMatrix::sortColumns ( bool sort_rows = false )

inline

Sorts in ascending column order.

Sorts all elements so that they appear in ascending column order in the internal arrays.

◆ sortRows()

void goSparseMatrix::sortRows ( bool sort_columns = false )

inline

Sorts in ascending row order.

Sorts all elements so that they appear in ascending row order in the internal arrays.

◆ stencil()

template<class T >

T goMath::stencil	(	const goSignal3DBase< void > &	sig,
		const goMath::Matrix< T > &	s
	)

Calculate 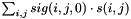$\sum_{i,j} sig(i,j,0) \cdot s(i,j)$ .

Can be used to calculate a sum of a 2D stencil multiplied by the values in sig. Only the z=0 plane is accounted for in sig. You can for example have a goSubSignal3D move over a goSignal3DBase and calculate some weighted sum (in 2D) at each point of interest.

The sizes of sig and s should match.

Parameters

sig	Signal
s	Matrix containing the stencil.

Returns: The sum of the elements in sig weighted with s.

◆ transform2D()

void goMath::transform2D	(	const goSignal3DBase< void > &	source,
		goDouble	scale,
		goDouble	angle,
		goDouble	t_x,
		goDouble	t_y,
		goSignal3D< void > &	target,
		bool	setsize = `true`
	)

2D euclidean transformation of an image.

Calculate 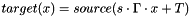$target(x) = source(s\cdot\Gamma\cdot x + T)$

Parameters

source	Source image (2D)
scale	Scale factor
angle	Rotation angle
t_x	Translation in x
t_y	Translation in y
target	Target, will be resized and set to the data type of `source` if necessary.
setsize	Automatically set size of target if it does not fit. Default: true.

◆ vectorMatrixMult() [1/2]

bool goSparseMatrix::vectorMatrixMult	(	goArray< goDouble > &	ret,
		const goArray< goDouble > &	v
	)

inline

v' * (this)

Parameters

ret
v

Returns

◆ vectorMatrixMult() [2/2]

bool goSparseMatrix::vectorMatrixMult	(	goSparseMatrix &	ret,
		const goArray< goDouble > &	v
	)

inline

v' * (this)

Parameters

ret
v

Returns

Modules

Classes

Typedefs

Enumerations

Functions

Detailed Description

Typedef Documentation

◆ go4Vectorf

Function Documentation

◆ abs()

◆ acos()

◆ appendRow()

◆ appendRows()

◆ backwardDifferences()

◆ centralDifferences()

◆ ddx2D()

◆ ddy2D()

◆ euclideanToBarycentric()

◆ fillBegin()

◆ fillEnd()

◆ fillNext()

◆ forwardDifferences()

◆ getElementCount()

◆ goConjugateGradients()

◆ gradient2D()

◆ hypot()

◆ integrate()

◆ integrateSimpson()

◆ karcherMean()

◆ laplacian2D()

◆ matrixVectorMult() [1/4]

◆ matrixVectorMult() [2/4]

◆ matrixVectorMult() [3/4]

◆ matrixVectorMult() [4/4]

◆ max()

◆ min()

◆ mod()

◆ paste2D()

◆ resampleCubic()

◆ scale2D()

◆ set()

◆ sortColumns()

◆ sortRows()

◆ stencil()

◆ transform2D()

◆ vectorMatrixMult() [1/2]

◆ vectorMatrixMult() [2/2]