#include <gomatrix.h>
Public Types | |
| typedef T | value_type |
| typedef VectorIterator< T > | vector_iterator |
| typedef ConstVectorIterator< T > | const_vector_iterator |
Public Member Functions | |
| Matrix (goSize_t rows=4, goSize_t cols=4) | |
| Matrix (const Matrix< T > &other) | |
| Copy constructor. More... | |
| Matrix (T *data, goSize_t r, goSize_t c, goSize_t leadingDim=0) | |
| Constructor for using external data. More... | |
| vector_iterator | rowBegin () |
| Get an iterator to the first row. More... | |
| vector_iterator | rowEnd () |
| Get an iterator pointing after the last row. More... | |
| const_vector_iterator | rowBegin () const |
| Get an iterator to the first row. More... | |
| const_vector_iterator | rowEnd () const |
| Get an iterator pointing after the last row. More... | |
| vector_iterator | colBegin () |
| Get an iterator to the first column. More... | |
| vector_iterator | colEnd () |
| Get an iterator pointing after the last column. More... | |
| const_vector_iterator | colBegin () const |
| Get an iterator to the first column. More... | |
| const_vector_iterator | colEnd () const |
| Get an iterator pointing after the last column. More... | |
| bool | setData (T *data, goSize_t r, goSize_t c, goSize_t leadingDim=0) |
| Set external data. More... | |
| bool | setData (const T *data, goSize_t r, goSize_t c, goSize_t leadingDim=0) const |
| bool | resize (goSize_t rows, goSize_t cols) |
| Resize (re-allocate) the matrix. More... | |
| bool | reshape (goSize_t rows, goSize_t cols) |
| Reshape this matrix as long as the new shape results in the same total number of elements. More... | |
| template<class To > | |
| bool | resize (const Matrix< To > &o) |
| bool | transpose () |
| Transpose the data. This is very slow and should be used scarcely. For Multiplication with transposition, use goMath::MatrixMult(). | |
| bool | getTranspose (Matrix< T > &trans) const |
| Get a transposed copy of this matrix. More... | |
| Matrix< T > | getTranspose () const |
| bool | invert () |
| void | power (T scalar) |
| void | flip (goSize_t dim=0) |
| Flip in row or column direction. More... | |
| void | shiftRows (goIndex_t offset, Matrix< T > &ret) const |
| Shift (cyclically permute) rows. More... | |
| void | shiftColumns (goIndex_t offset, Matrix< T > &ret) const |
| Shift (cyclically permute) columns. More... | |
| Matrix< T > & | operator= (const Matrix< T > &other) |
| Deep copy operator. More... | |
| bool | operator== (const Matrix< T > &other) const |
| bool | operator!= (const Matrix< T > &other) const |
| T * | getData () |
| Get data pointer. More... | |
| const T * | getData () const |
| Get data pointer. More... | |
| T * | getPtr () |
| Get data pointer. Same as getData(). | |
| const T * | getPtr () const |
| Get data pointer. Same as getData(). | |
| goSize_t | getColumns () const |
| Get number of columns. More... | |
| goSize_t | getRows () const |
| Get number of rows. More... | |
| goSize_t | getLeadingDimension () const |
| Get the leading dimension. In row major order, this is the number of columns. This can be directly used as LDX parameter in CBLAS routines. From http://www.inf.bv.tum.de/~heisserer/softwarelab04/index.html "Note that for cblas-functions the leading dimension (for 2D arrays in C-fashion, i.e. row major order) is the number of columns of the matrix (not the rows as in Fortran). The leading dimension is the number of entries in memory that separate the e.g. first elements of rows in c-fashion storage (row major order, i.e. elements of one row are contiguous in memory). As Fortran stores in column major order the leading dimension is the number of rows.". More... | |
| T | sum () const |
| Sum over all elements. More... | |
| void | sum (int dimension, Matrix< T > &ret) const |
| Sum over all columns / all rows. More... | |
| void | sum (int dimension, goMath::Vector< T > &ret) const |
| int | dim1 () const |
| int | dim2 () const |
| const Matrix< T > & | copy () const |
| void | ref (goSize_t startRow, goSize_t startColumn, goSize_t num_rows, goSize_t num_cols, Matrix< T > &refMatrix) |
| Make a reference to sub-matrix. More... | |
| bool | copy (goSize_t startRow, goSize_t startCol, goSize_t endRow, goSize_t endCol, Matrix< T > &target, bool trans=false) const |
| Copies sub-matrix from this matrix to target matrix. More... | |
| bool | copy (goSize_t startRow, goSize_t startCol, goSize_t endRow, goSize_t endCol, goSize_t target_row, goSize_t target_col, Matrix< T > &target, bool trans=false) const |
| Copy rectangular sub-matrix to another matrix. More... | |
| bool | copy (Matrix< T > &target) const |
| Copies this matrix to target matrix. More... | |
| void | ref (goSize_t startRow, goSize_t startColumn, goSize_t num_rows, goSize_t num_cols, const Matrix< T > &refMatrix) const |
| Make a reference to sub-matrix. More... | |
| void | refRow (goSize_t row, goMath::Vector< T > &v) |
| Makes a vector reference a row from this matrix. More... | |
| void | refRow (goSize_t row, goSize_t column, goSize_t length, goMath::Vector< T > &v) |
| Reference to a sub row. More... | |
| void | setRow (goSize_t row, const goMath::Vector< T > &v) |
| void | setColumn (goSize_t col, const goMath::Vector< T > &v) |
| void | refRow (goSize_t row, const goMath::Vector< T > &v) const |
| Const reference to row. More... | |
| void | refRow (goSize_t row, goSize_t column, goSize_t length, const goMath::Vector< T > &v) const |
| Reference to a sub row. More... | |
| void | refColumn (goSize_t column, goMath::Vector< T > &v) |
| Makes a vector reference a column from this matrix. More... | |
| void | refColumn (goSize_t row, goSize_t column, goSize_t length, goMath::Vector< T > &v) |
| Reference to a sub column. More... | |
| void | refColumn (goSize_t column, const goMath::Vector< T > &v) const |
| Const reference to column. More... | |
| void | refColumn (goSize_t row, goSize_t column, goSize_t length, const goMath::Vector< T > &v) const |
| Reference to a sub column. More... | |
| template<class To > | |
| void | copyRow (goSize_t row, goMath::Vector< To > &vRet) const |
| Copies a row to vector vRet. More... | |
| template<class To > | |
| void | copyColumn (goSize_t col, goMath::Vector< To > &vRet) const |
| Copied a column to vector vRet. More... | |
| void | swapRows (goIndex_t i1, goIndex_t i2) |
| void | swapColumns (goIndex_t i1, goIndex_t i2) |
| T & | operator() (goIndex_t i, goIndex_t j) |
| const T & | operator() (goIndex_t i, goIndex_t j) const |
| void | operator() (goIndex_t i1, goIndex_t j1, goIndex_t i2, goIndex_t j2, Matrix< T > &target) const |
| References sub-matrix from i1,j1 to i2,j2 into target. More... | |
| void | operator() (const Matrix< T > &source, goIndex_t i1, goIndex_t j1, goIndex_t i2, goIndex_t j2) |
| Copy source to sub-matrix from i1,j1 to i2,j2 in this matrix. More... | |
| T & | operator[] (goSize_t index) |
| const T & | operator[] (goSize_t index) const |
| Matrix< T > | operator* (const Matrix< T > &other) const |
| Matrix multiplication. More... | |
| Matrix< T > | operator- (const Matrix< T > &other) const |
| Matrix< T > | operator+ (const Matrix< T > &other) const |
| Matrix< T > & | operator*= (const Matrix< T > &other) |
| this = this * other More... | |
| Matrix< T > & | operator+= (const Matrix< T > &other) |
| Element-wise addition. More... | |
| Matrix< T > & | operator+= (T scalar) |
| Matrix< T > & | operator-= (const Matrix< T > &other) |
| Element-wise subtraction. More... | |
| Matrix< T > & | operator-= (T scalar) |
| goMath::Vector< T > | operator* (const goMath::Vector< T > &v) const |
| Matrix vector multiplication. More... | |
| Matrix< T > & | operator*= (T scalar) |
| Multiplication by a scalar. More... | |
| Matrix< T > | operator* (T scalar) |
| Matrix< T > & | operator/= (T scalar) |
| Division by a scalar. More... | |
| bool | multiplyElements (const Matrix< T > &other) |
| Element-wise multiplication. More... | |
| T | norm () const |
Calculate the Frobenius norm  where where 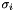 is the is the 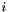 'th singular value. More... 'th singular value. More... | |
| T | trace () const |
Calculates the trace 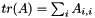 . More... . More... | |
| void | setUnity () |
| Load identity matrix. | |
| void | setIdentity () |
| Load identity matrix. | |
| void | fill (T v) |
| Fill matrix with a value v. More... | |
| void | print () const |
| bool | writeASCII (FILE *f) const |
| bool | writeASCII (const char *fname) const |
| bool | readASCII (FILE *f) |
| bool | readASCIISimple (FILE *f) |
| bool | readASCII (const char *f) |
| template<> | |
| goMath::Matrix< goDouble > | operator* (const goMath::Matrix< goDouble > &other) const |
| template<> | |
| goMath::Matrix< goFloat > | operator* (const goMath::Matrix< goFloat > &other) const |
| template<> | |
| Matrix< goFloat > & | operator*= (const Matrix< goFloat > &other) |
| template<> | |
| Matrix< goDouble > & | operator*= (const Matrix< goDouble > &other) |
| template<> | |
| goMath::Vector< goFloat > | operator* (const goMath::Vector< goFloat > &v) const |
| template<> | |
| goMath::Vector< goDouble > | operator* (const goMath::Vector< goDouble > &v) const |
| template<> | |
| goComplexf | trace () const |
| template<> | |
| void | power (goFloat scalar) |
| template<> | |
| void | power (goDouble scalar) |
| template<> | |
| goComplexf | norm () const |
| template<> | |
| bool | writeASCII (FILE *f) const |
| template<> | |
| bool | readASCII (FILE *f) |
| template<> | |
| bool | invert () |
| template<> | |
| bool | invert () |
Static Public Attributes | |
| static const bool | rowMajor = goMath::rowMajor |
Protected Attributes | |
| bool | externalData |
| T * | matrix |
| goSize_t | rows |
| goSize_t | columns |
| goSize_t | leadingDimension |
Detailed Description
template<class T>
class goMath::Matrix< T >
Matrix class.
This class uses linear data storage, row major, i.e. rows are contigious in memory. It is designed to be compatible with CBLAS operations. Leading dimension in CBLAS is here the number of columns – get it via getLeadingDimension().
There is no support for [i][j] indexing anymore. Use (i,j) instead.
- Examples
- karchermean/km.cpp, and so3/so3.cpp.
Constructor & Destructor Documentation
◆ Matrix() [1/3]
| goMath::Matrix< T >::Matrix | ( | goSize_t | r = 4, |
| goSize_t | c = 4 |
||
| ) |
- Parameters
-
y Number of rows. x Number of columns.
◆ Matrix() [2/3]
| goMath::Matrix< T >::Matrix | ( | const Matrix< T > & | other | ) |
Copy constructor.
- Parameters
-
other Other matrix. Will be deep copied.
◆ Matrix() [3/3]
| goMath::Matrix< T >::Matrix | ( | T * | data, |
| goSize_t | r, | ||
| goSize_t | c, | ||
| goSize_t | leadingDim = 0 |
||
| ) |
Constructor for using external data.
- Parameters
-
data Pointer to the external data. r Rows c Columns leadingDim leading dimension – if 0, is set to c. data Pointer to the external data. r Rows c Columns
Member Function Documentation
◆ colBegin() [1/2]
| goMath::Matrix< T >::vector_iterator goMath::Matrix< T >::colBegin | ( | ) |
Get an iterator to the first column.
- Returns
- Vector iterator to the first column.
◆ colBegin() [2/2]
| goMath::Matrix< T >::const_vector_iterator goMath::Matrix< T >::colBegin | ( | ) | const |
Get an iterator to the first column.
- Returns
- Vector iterator to the first column.
◆ colEnd() [1/2]
| goMath::Matrix< T >::vector_iterator goMath::Matrix< T >::colEnd | ( | ) |
Get an iterator pointing after the last column.
- Returns
- Iterator pointing after the last column.
◆ colEnd() [2/2]
| goMath::Matrix< T >::const_vector_iterator goMath::Matrix< T >::colEnd | ( | ) | const |
Get an iterator pointing after the last column.
- Returns
- Iterator pointing after the last column.
◆ copy() [1/3]
| bool goMath::Matrix< T >::copy | ( | goSize_t | startRow, |
| goSize_t | startCol, | ||
| goSize_t | endRow, | ||
| goSize_t | endCol, | ||
| goSize_t | target_row, | ||
| goSize_t | target_col, | ||
| goMath::Matrix< T > & | target, | ||
| bool | trans = false |
||
| ) | const |
Copy rectangular sub-matrix to another matrix.
Copies from this matrix the sub-matrix (startRow...endRow , startCol...endCol) to the sub-matrix in target starting at target_row,target_col.
Does not do resizing. If the target is too small, nothing is copied.
- Parameters
-
startRow Starting row in this matrix. startCol Starting column in this matrix. endRow End row in this matrix (inclusive) endCol End column in this matrix (inclusive) target_row Starting row in target target_col Starting column in target target Target matrix trans Transpose while copying (target = transpose(this))
- Returns
- True if successful, false otherwise.
◆ copy() [2/3]
| bool goMath::Matrix< T >::copy | ( | goSize_t | startRow, |
| goSize_t | startCol, | ||
| goSize_t | endRow, | ||
| goSize_t | endCol, | ||
| goMath::Matrix< T > & | target, | ||
| bool | trans = false |
||
| ) | const |
Copies sub-matrix from this matrix to target matrix.
Copies the given sub-matrix from this to target starting in target at 0,0.
- Parameters
-
startRow startCol endRow endCol target trans Transpose while copying (target = transpose(this))
- Returns
- True if successful, false otherwise.
◆ copy() [3/3]
| bool goMath::Matrix< T >::copy | ( | goMath::Matrix< T > & | target | ) | const |
Copies this matrix to target matrix.
Target is not resized, this matrix is copied to target starting at 0,0. If target is too small, false is returned.
- Parameters
-
target
- Returns
- True if successful, false otherwise.
◆ copyColumn()
|
inline |
◆ copyRow()
|
inline |
Copies a row to vector vRet.
vRet is resized if it vRet.getSize() != this->getColumns().
- Parameters
-
row Row to copy. vRet Vector.
◆ fill()
| void goMath::Matrix< T >::fill | ( | T | v | ) |
Fill matrix with a value v.
- Parameters
-
v Value to fill with.
◆ flip()
| void goMath::Matrix< T >::flip | ( | goSize_t | dim = 0 | ) |
Flip in row or column direction.
- Parameters
-
dim If 0, flips rows, otherwise flips columns.
◆ getColumns()
|
inline |
Get number of columns.
- Returns
- Number of columns.
◆ getData() [1/2]
|
inline |
Get data pointer.
- Returns
- Pointer to the matrix array.
◆ getData() [2/2]
|
inline |
Get data pointer.
- Returns
- Const pointer to the matrix array.
◆ getLeadingDimension()
|
inline |
Get the leading dimension. In row major order, this is the number of columns. This can be directly used as LDX parameter in CBLAS routines.
From http://www.inf.bv.tum.de/~heisserer/softwarelab04/index.html
"Note that for cblas-functions the leading dimension (for 2D arrays in C-fashion, i.e. row major order) is the number of columns of the matrix (not the rows as in Fortran). The leading dimension is the number of entries in memory that separate the e.g. first elements of rows in c-fashion storage (row major order, i.e. elements of one row are contiguous in memory). As Fortran stores in column major order the leading dimension is the number of rows.".
- Returns
- Leading dimension.
◆ getRows()
|
inline |
Get number of rows.
- Returns
- Number of rows.
◆ getTranspose()
| bool goMath::Matrix< T >::getTranspose | ( | goMath::Matrix< T > & | trans | ) | const |
Get a transposed copy of this matrix.
- Parameters
-
trans Contains the transpose after the method returned.
◆ multiplyElements()
| bool goMath::Matrix< T >::multiplyElements | ( | const Matrix< T > & | other | ) |
Element-wise multiplication.
this . other
- Parameters
-
other Other matrix.
- Returns
- True
◆ norm()
| T goMath::Matrix< T >::norm | ( | ) | const |
Calculate the Frobenius norm  where
where 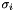 is the
is the 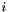 'th singular value.
'th singular value.
- Returns
- The Frobenius norm of this matrix.
◆ operator()() [1/2]
| void goMath::Matrix< T >::operator() | ( | const Matrix< T > & | source, |
| goIndex_t | i1, | ||
| goIndex_t | j1, | ||
| goIndex_t | i2, | ||
| goIndex_t | j2 | ||
| ) |
Copy source to sub-matrix from i1,j1 to i2,j2 in this matrix.
- Note
- Dimensions must agree and are assert()ed. Check logfile for warnings.
◆ operator()() [2/2]
| void goMath::Matrix< T >::operator() | ( | goIndex_t | i1, |
| goIndex_t | j1, | ||
| goIndex_t | i2, | ||
| goIndex_t | j2, | ||
| goMath::Matrix< T > & | target | ||
| ) | const |
References sub-matrix from i1,j1 to i2,j2 into target.
To make clear it is referencing, use the ref() method.
◆ operator*() [1/2]
| goMath::Vector< T > goMath::Matrix< T >::operator* | ( | const goMath::Vector< T > & | v | ) | const |
Matrix vector multiplication.
- Note
- Uses CBLAS for goFloat and goDouble types.
- Parameters
-
v A vector.
- Returns
- (*this) * v
◆ operator*() [2/2]
| goMath::Matrix< T > goMath::Matrix< T >::operator* | ( | const Matrix< T > & | other | ) | const |
Matrix multiplication.
- Note
- Uses CBLAS for goFloat and goDouble types.
- See also
- MatrixMult()
- Parameters
-
other A matrix.
- Returns
- this * other
◆ operator*=() [1/2]
| goMath::Matrix< T > & goMath::Matrix< T >::operator*= | ( | const Matrix< T > & | other | ) |
this = this * other
- Note
- Uses CLBLAS for goFloat and goDouble types.
- See also
- goMath::MatrixMult()
- Parameters
-
other A Matrix.
- Returns
- Reference to this.
◆ operator*=() [2/2]
|
inline |
Multiplication by a scalar.
- Parameters
-
scalar A scalar.
- Returns
- this .* scalar.
◆ operator+=()
| goMath::Matrix< T > & goMath::Matrix< T >::operator+= | ( | const Matrix< T > & | other | ) |
Element-wise addition.
- Parameters
-
other
- Returns
- this = this + other
◆ operator-=()
| goMath::Matrix< T > & goMath::Matrix< T >::operator-= | ( | const Matrix< T > & | other | ) |
Element-wise subtraction.
- Parameters
-
other
- Returns
- this = this - other
◆ operator/=()
|
inline |
Division by a scalar.
- Parameters
-
scalar
- Returns
- this ./ scalar.
◆ operator=()
| goMath::Matrix< T > & goMath::Matrix< T >::operator= | ( | const Matrix< T > & | other | ) |
Deep copy operator.
If the size of this matrix does not match, it will be resized (ref()'ed matrices will no longer be references!). If the size matches, nothing is changed and data are just copied.
- Parameters
-
other Other matrix.
- Returns
- Reference to this matrix.
◆ ref() [1/2]
|
inline |
Make a reference to sub-matrix.
refMatrix will be initialised to refer to the sub-matrix starting at (startRow,startColumn) and extending for num_rows and num_cols rows and columns, respectively.
- Note
- No bound checks are done.
- Parameters
-
startRow Start element. startColumn Start element. num_rows Number of rows. num_cols Number of columns. refMatrix Refers to the defined sub-matrix on return.
◆ ref() [2/2]
|
inline |
Make a reference to sub-matrix.
refMatrix will be initialised to refer to the sub-matrix starting at (startRow,startColumn) and extending for num_rows and num_cols rows and columns, respectively.
- Note
- No bound checks are done.
- Parameters
-
startRow Start element. startColumn Start element. num_rows Number of rows. num_cols Number of columns. refMatrix Refers to the defined sub-matrix on return.
◆ refColumn() [1/4]
|
inline |
Const reference to column.
- Note
- Argument v will be changed even though it is const. This is just to provide a consistent way to reference rows and columns in const matrices. It may be bad style from one point of view, on the other hand it enables referencing without further hassle.
- Parameters
-
column Column index. v WILL BE CHANGED and contains the reference.
◆ refColumn() [2/4]
|
inline |
Makes a vector reference a column from this matrix.
- Note
- The data are not copied.
- Parameters
-
column Column to reference v Vector that holds the reference after the method returns.
◆ refColumn() [3/4]
|
inline |
Reference to a sub column.
- Parameters
-
row Start element row column Start element column length length of vector v Vector that contains the reference after the method call.
◆ refColumn() [4/4]
|
inline |
Reference to a sub column.
- Parameters
-
row Start element row column Start element column length length of vector v Vector that contains the reference after the method call.
◆ refRow() [1/4]
|
inline |
Const reference to row.
- Note
- Argument v will be changed even though it is const. This is just to provide a consistent way to reference rows and columns in const matrices. It may be bad style from one point of view, on the other hand it enables referencing without further hassle.
- Parameters
-
row Row index. v WILL BE CHANGED and contains the reference.
◆ refRow() [2/4]
|
inline |
Makes a vector reference a row from this matrix.
- Note
- The data are not copied.
- Parameters
-
row Row to reference v Vector that holds the reference after the method returns.
◆ refRow() [3/4]
|
inline |
Reference to a sub row.
- Parameters
-
row Start element row column Start element column length length of vector v Vector that contains the reference after the method call.
◆ refRow() [4/4]
|
inline |
Reference to a sub row.
- Parameters
-
row Start element row column Start element column length length of vector v Vector that contains the reference after the method call.
◆ reshape()
| bool goMath::Matrix< T >::reshape | ( | goSize_t | rows, |
| goSize_t | cols | ||
| ) |
Reshape this matrix as long as the new shape results in the same total number of elements.
If the number rows*cols is the same as this->getRows()*this->getColumns(), the matrix is reshaped; the data are not touched in any way. Nothing is reallocated.
- Parameters
-
rows Number of rows of the new shape cols Number of columns of the new shape
- Returns
- True on success, false otherwise.
◆ resize()
| bool goMath::Matrix< T >::resize | ( | goSize_t | rows, |
| goSize_t | cols | ||
| ) |
Resize (re-allocate) the matrix.
Memory is newly allocated, so all former data is lost.
- Parameters
-
rows Rows. cols Columns.
- Returns
- True if successful, false otherwise. Currently always true.
◆ rowBegin() [1/2]
| goMath::Matrix< T >::vector_iterator goMath::Matrix< T >::rowBegin | ( | ) |
Get an iterator to the first row.
- Returns
- Vector iterator to the first row.
◆ rowBegin() [2/2]
| goMath::Matrix< T >::const_vector_iterator goMath::Matrix< T >::rowBegin | ( | ) | const |
Get an iterator to the first row.
- Returns
- Vector iterator to the first row.
◆ rowEnd() [1/2]
| goMath::Matrix< T >::vector_iterator goMath::Matrix< T >::rowEnd | ( | ) |
Get an iterator pointing after the last row.
- Returns
- Iterator pointing after the last row.
◆ rowEnd() [2/2]
| goMath::Matrix< T >::const_vector_iterator goMath::Matrix< T >::rowEnd | ( | ) | const |
Get an iterator pointing after the last row.
- Returns
- Iterator pointing after the last row.
◆ setData()
| bool goMath::Matrix< T >::setData | ( | T * | data, |
| goSize_t | r, | ||
| goSize_t | c, | ||
| goSize_t | leadingDim = 0 |
||
| ) |
Set external data.
- Parameters
-
data Pointer to the external data. r Rows c Columns
- Returns
- True.
◆ shiftColumns()
| void goMath::Matrix< T >::shiftColumns | ( | goIndex_t | offset, |
| goMath::Matrix< T > & | ret | ||
| ) | const |
Shift (cyclically permute) columns.
Shifts all columns "down" a given offset. The offset can be positive or negative
- Parameters
-
offset Offset ret On return, contains the shifted matrix.
◆ shiftRows()
| void goMath::Matrix< T >::shiftRows | ( | goIndex_t | offset, |
| goMath::Matrix< T > & | ret | ||
| ) | const |
Shift (cyclically permute) rows.
Shifts all rows "down" a given offset. The offset can be positive or negative
- Parameters
-
offset Offset ret On return, contains the shifted matrix.
◆ sum() [1/2]
| T goMath::Matrix< T >::sum | ( | ) | const |
Sum over all elements.
- Returns
- Sum over all elements.
◆ sum() [2/2]
| void goMath::Matrix< T >::sum | ( | int | dimension, |
| goMath::Matrix< T > & | ret | ||
| ) | const |
Sum over all columns / all rows.
- Parameters
-
dimension If 0, sums over all columns and the result is a row vector. Else, sums over all rows and the result is a column vector. ret Result.
◆ trace()
| T goMath::Matrix< T >::trace | ( | ) | const |
Calculates the trace 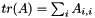 .
.
Works also for non-square matrices; in that case, the loop runs to the smaller of the two dimensions.
- Returns
- The trace of the matrix.
The documentation for this class was generated from the following files:
- gomatrix.h
- gomatrix.cpp
