Classes
class	goMath::Eigenvalue< Real >
	Eigenvalue computation of real matrices. More...

class	goMath::LU< Real >
	LU Decomposition. More...

class	goMath::VectorIterator< T >
	Vector iterator for multi-dimensional array data. More...

class	goMath::ConstVectorIterator< T >
	Cons iterator over vectors. More...

class	goMath::Matrix< T >
	Matrix class. More...

class	goMath::SVD< T >
	Singular value decomposition. This class can do full SVD or thin SVD. It uses sgesvd_() or dgesvd_() from the linked LAPACK library (as opposed to goMath::ThinSVD). Instantiated for goFloat and goDouble types. More...

class	goMath::Vector< T >
	General vector class. More...

Typedefs
typedef goMath::Matrix< goDouble >	goMath::Matrixd

typedef goMath::Matrix< goFloat >	goMath::Matrixf

typedef goMath::Vector< goFloat >	goMath::Vectorf

typedef goMath::Vector< goDouble >	goMath::Vectord

typedef goMath::Vector< goInt32 >	goMath::Vectori

Functions
goSize_t	goMath::complexEigenvaluesHermite (const goMath::Matrix< goComplexf > &m, goMath::Vectorf &eigenvaluesRet, goFixedArray< goMath::Vector< goComplexf > > *eigenvectorsRet=0)

template<class T >
void	goMath::matrixMult (T alpha, const goMath::Matrix< T > &A, bool transA, const goMath::Matrix< T > &B, bool transB, T beta, goMath::Matrix< T > &C)
	Calculate 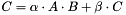$C = \alpha \cdot A \cdot B + \beta \cdot C$ . More...

template<class T >
void	goMath::matrixPower (goMath::Matrix< T > &A, T scalar)

template<class T >
bool	goMath::matrixVectorMult (T alpha, const goMath::Matrix< T > &A, bool transA, const goMath::Vector< T > &x, T beta, goMath::Vector< T > &y)
	calculate 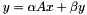$y = \alpha A x + \beta y$ . More...

template<class T >
bool	goMath::vectorAdd (T alpha, const Vector< T > &x, Vector< T > &y)
	y = alpha * x + y More...

template<class T >
void	goMath::vectorOuter (T alpha, const Vector< T > &x, const Vector< T > &y, goMath::Matrix< T > &ret)
	Outer vector product 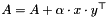$A = A + \alpha \cdot x \cdot y^\top$ . More...

template<class matrix_type , class pivot_vector >
bool	goMath::Lapack::getrf (matrix_type &A, pivot_vector &ipiv)
	Lapack getrf. More...

template<class matrix_type , class pivot_vector >
bool	goMath::Lapack::getrs (const matrix_type &A, bool transA, matrix_type &B, const pivot_vector &ipiv)
	Lapack getrs. More...

template<class matrix_type , class pivot_vector >
bool	goMath::Lapack::getrs (const matrix_type &A, bool transA, goMath::Vector< typename matrix_type::value_type > &B, const pivot_vector &ipiv)

template<class matrix_type , class pivot_vector >
bool	goMath::Lapack::getri (matrix_type &A, const pivot_vector &ipiv)
	Lapack getri, invert a LU-decomposed matrix. More...

template<class matrix_type , class vector_type >
bool	goMath::Lapack::gels (matrix_type &A, bool transA, vector_type &b)
	Lapack gels. Least square solution of a linear system. More...

template<class matrix_type , class vector_type >
bool	goMath::Lapack::gelss (matrix_type &A, bool transA, vector_type &b, vector_type *singularValues=0)
	Lapack gelss. More...

template<class matrix_type , class vector_type >
bool	goMath::Lapack::posv (matrix_type &A, vector_type &b)
	Lapack *posv procedure for solving symmetric linear systems. More...

template<class matrix_type >
bool	goMath::Lapack::posv (matrix_type &A, matrix_type &b)
	Lapack *posv procedure for solving symmetric linear systems. More...

T	goMath::Vector< T >::conjInnerProduct (const Vector< T > &) const

Detailed Description

Linear Algebra Objects

Use goMatrix and goVector for matrix and vector operations. Others, like go4Vector and such will be deprecated and replaced solely by the former two classes. goMatrix and goVector use CBLAS routines for some operations and more will be added. Using CBLAS moves the matter of optimisation for a specific platform outside of golib. The operator* and operator*= operators use CBLAS. For best performance, when you want to do something like C = A^\top \cdot B + C, use goMatrixMult(). Explicitly transposing a matrix should not be necessary, if I find it is for some operation, I will add functions that overcome this. Transposition of a goMatrix is possible with getTranspose() or transpose(), but is very slow since the data are copied.

Singular value decomposition can be done using goSVD. Eigenvalues and eigenvectors can be calculated with goEigenvalue. Both are adapted versions from the Template Numerical Toolkit, a freely available implementation of a few linear algebra algorithms.

Function Documentation

◆ gels()

template<class matrix_type , class vector_type >

bool goMath::Lapack::gels	(	matrix_type &	A,
		bool	transA,
		vector_type &	b
	)

Lapack gels. Least square solution of a linear system.

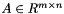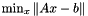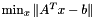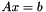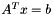For $A \in R^{m \times n}$ solves $\min_x \|Ax - b\|$ or $\min_x \|A^T x - b\|$ if m >= n, or it finds the minimum norm solution of $ Ax = b $ or $ A^T x = b $ if m < n, so that 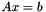$ Ax = b$ is underdetermined. A must have full rank.

Parameters

A	Matrix A. Will be overwritten by QR or LQ decompositions.
transA	If true, A is used transposed.
b	Right hand side vector. Will be overwritten with the solution vector.

Returns: True if successful, false otherwise.

Bug:: Appears not to work – needs testing (examples/lapack.cpp)

◆ gelss()

template<class matrix_type , class vector_type >

bool goMath::Lapack::gelss	(	matrix_type &	A,
		bool	transA,
		vector_type &	b,
		vector_type *	singularValues = `0`
	)

Lapack gelss.

Note: NEEDS TESTING, UNTESTED. Possibly the LDA is wrong if the matrix is not square (which is true in general).

Parameters

A
transA
b
singularValues

Returns

◆ getrf()

template<class matrix_type , class pivot_vector >

bool goMath::Lapack::getrf	(	matrix_type &	A,
		pivot_vector &	ipiv
	)

Lapack getrf.

Note: Uses ATLAS' clapack implementation.

Replaces A by its LU-decomposed form, 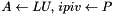$A \gets LU, \, ipiv \gets P$ so that 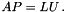$AP = LU \, .$ U is unit diagonal, P pivots columns.

Parameters

A	Matrix to be decomposed.
ipiv	Pivot vector (filled by this function).

Returns: True if successful, false otherwise.

◆ getri()

template<class matrix_type , class pivot_vector >

bool goMath::Lapack::getri	(	matrix_type &	A,
		const pivot_vector &	ipiv
	)

Lapack getri, invert a LU-decomposed matrix.

Note: Uses ATLAS' clapack implementation.

The matrix must be in LU-form created by getrf().

Parameters

A	Matrix to invert. Must be in LU form and must be quadratic.
ipiv	Pivot vector as created by getrf().

Returns: True if successful, false otherwise.

◆ getrs()

template<class matrix_type , class pivot_vector >

bool goMath::Lapack::getrs	(	const matrix_type &	A,
		bool	transA,
		matrix_type &	B,
		const pivot_vector &	ipiv
	)

Lapack getrs.

Note: Uses ATLAS' clapack implementation.

Solves 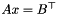$A x = B^\top$ for x, assuming A is LU-decomposed e.g. with getrf(). Implemented for goFloat and goDouble. pivot_vector must be of type int, and provide getSize(), resize() as well as getPtr() methods (such as goMath::Vector). matrix_type must essentially be goMath::Matrix.

Note: B contains the right hand side vectors in its rows. Always remember this. This is apparently an effect of using row major order which stems from ATLAS.

Parameters

A	Matrix A
transA	Use A transposed
B	Right hand side (the right hand side vectors are in the `rows` of B, not the columns!). On success, the rows contain the solutions.
ipiv	Pivot vector (from getrf()).

Returns: True if successful, false otherwise.

◆ matrixMult()

template<class T >

void goMath::matrixMult	(	T	alpha,
		const goMath::Matrix< T > &	A,
		bool	transA,
		const goMath::Matrix< T > &	B,
		bool	transB,
		T	beta,
		goMath::Matrix< T > &	C
	)

Calculate 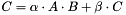$C = \alpha \cdot A \cdot B + \beta \cdot C$ .

A and B can optionally be used as transpose. This function uses CBLAS functions.

This function is implemented for goFloat and goDouble, using cblas_[s|d]gemm functions from CBLAS.

Parameters

alpha	Multiplicative factor for A
A	Matrix A
transA	If true, A will be used transposed.
B	Matrix B
transB	If true, B will be used transposed.
beta	Multiplicative factor for C
C	Matrix C, also holds the result.

◆ matrixVectorMult()

template<class T >

bool goMath::matrixVectorMult	(	T	alpha,
		const goMath::Matrix< T > &	A,
		bool	transA,
		const goMath::Vector< T > &	x,
		T	beta,
		goMath::Vector< T > &	y
	)

calculate 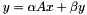$y = \alpha A x + \beta y$ .

Sizes of A and x are checked. If y has mismatching size, it is resized and initialised with 0 before the operation.

Parameters are named as in the formula above.

Uses cblas_<>gemv().

Todo:: TEST THIS FUNCTION.

Parameters

alpha	Scalar factor
A	Matrix A
transA	If true, A is used as transposed.
x	Vector x
beta	Scalar factor (for y)
y	Vector y, also holds the result.

Returns: true if successful, false otherwise.

◆ posv() [1/2]

template<class matrix_type >

bool goMath::Lapack::posv	(	matrix_type &	A,
		matrix_type &	b
	)

Lapack *posv procedure for solving symmetric linear systems.

Parameters

A	Symmetric matrix, no special storage, must be upper right.
b	Contains the right hand side vectors in its rows. This is due to the actual lapack routine using column major storage and we use the more C-like row major. Contains the solutions if the method returns true. The solutions are contained in the rows, again because of the underlying routine using column major storage.

Returns: True if successful, false otherwise.

◆ posv() [2/2]

template<class matrix_type , class vector_type >

bool goMath::Lapack::posv	(	matrix_type &	A,
		vector_type &	b
	)

Lapack *posv procedure for solving symmetric linear systems.

Parameters

A	Symmetric matrix, no special storage, must be upper right.
b	Right hand side vector. Contains the solution if the method returns true.

Returns: True if successful, false otherwise.

◆ vectorAdd()

template<class T >

bool goMath::vectorAdd	(	T	alpha,
		const Vector< T > &	x,
		Vector< T > &	y
	)

y = alpha * x + y

Note: Implemented for goDouble and goFloat

Uses cblas_<>axpy functions. Sizes of x and y must match and are checked for.

Parameters

alpha	Scalar factor
x	Vector x
y	Vector y

Returns: True if successful, false otherwise.

◆ vectorOuter()

template<class T >

void goMath::vectorOuter	(	T	alpha,
		const Vector< T > &	x,
		const Vector< T > &	y,
		goMath::Matrix< T > &	ret
	)

Outer vector product 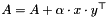$A = A + \alpha \cdot x \cdot y^\top$ .

Note: Implemented for goDouble and goFloat using cblas_<>ger(). Other types are directly implemented and therefore slower in most implementations.

Parameters

alpha	Scalar factor
x	Vector x of size M
y	Vector y of size N
ret	Return matrix A, of size MxN. Resized and initialised to 0 if it does not have the right size.

Classes

Typedefs

Functions

Detailed Description

Linear Algebra Objects

Function Documentation

◆ gels()

◆ gelss()

◆ getrf()

◆ getri()

◆ getrs()

◆ matrixMult()

◆ matrixVectorMult()

◆ posv() [1/2]

◆ posv() [2/2]

◆ vectorAdd()

◆ vectorOuter()