This module contains optimisation methods for Newton type optimisation. More...

Classes
class	goMath::NewtonOpt< type_ >
	Newton optimisation. More...

class	goMath::NewtonOptEq< type_ >
	Newton optimisation with linear equality constraints. More...

class	goMath::LineSearch< callable_, vector_type >

class	goMath::OptFunction< matrix_type, vector_type >
	Function interface for Newton type optimisation. More...

class	goMath::OptFunctor< matrix_type, vector_type >
	Convenience class taking a functor and providing the OptFunction interface. More...

class	goMath::OptProblem< matrix_type, vector_type >

Functions
template<class callable_ , class vector_type >
vector_type::value_type	goMath::backtrackingLineSearch (callable_ &f, typename vector_type::value_type f_x, const vector_type &nabla_f_x, const vector_type &x, const vector_type &dx, typename vector_type::value_type t=1, typename vector_type::value_type alpha=0.2, typename vector_type::value_type beta=0.8)
	Backtracking line search. More...

Detailed Description

This module contains optimisation methods for Newton type optimisation.

Function Documentation

template<class callable_ , class vector_type >

vector_type::value_type goMath::backtrackingLineSearch	(	callable_ &	f,
		typename vector_type::value_type	f_x,
		const vector_type &	nabla_f_x,
		const vector_type &	x,
		const vector_type &	dx,
		typename vector_type::value_type	t = `1`,
		typename vector_type::value_type	alpha = `0.2`,
		typename vector_type::value_type	beta = `0.8`
	)

Backtracking line search.

Searches for a sufficient decrease of f(x) in direction -dx, by repeating

$t = \beta \, t$

until

$f(x - t \, \Delta x) > f(x) - \alpha \, t \, \nabla f(x)^\top \Delta x$

with

$\alpha \in (0, 0.5), \, \beta \in (0,1) \, .$

References: Boyd, S. & Vandenberghe, L.: Convex Optimization. Cambridge University Press, 2004

Note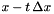: $x - t \, \Delta x$ must be in the domain of f, so in some cases it may be necessary to choose t accordingly when calling this function.

Parameters

callable_	Some callable object, i.e. allowing `vector_type::value_type callable_::operator() (const vector_type&)`
vector_type	A vector type, e.g. goMath::Vector<>
f	Function to evaluate
f_x	Value at point `x`
nabla_f_x	Value of the gradient of `f` at `x`
x	Point at which to evaluate
dx	Direction in which to evaluate
t	Starting parameter `t`, defaults to 1
alpha	Parameter `alpha`, defaults to 0.2
beta	Parameter `beta`, defaults to 0.8