golib  0.5
Public Types | Public Member Functions | Protected Attributes | List of all members
goMath::NewtonOpt< type_ > Class Template Reference
Mathematics and numerics » Optimisation

Newton optimisation. More...

#include <gonewton.h>

Public Types

typedef goMath::Vector< type_ > vector_type
 
typedef goMath::Matrix< type_ > matrix_type
 
typedef goMath::OptFunction< matrix_type, vector_type > function_type
 

Public Member Functions

 NewtonOpt (goAutoPtr< function_type > f)
 Constructor. More...
 
void setF (goAutoPtr< function_type > f)
 Sets the function to be minimised. More...
 
virtual void cleanup ()
 Frees temporary memory.
 
virtual void solveDirect (vector_type &x)
 Solves without line search. More...
 
virtual void solveLineSearch (vector_type &x)
 
virtual type_ newtonDecrement (vector_type &x)
 
virtual void step (vector_type &x, vector_type &ret)
 Calculate the newton step. More...
 

Protected Attributes

goAutoPtr< function_type > myF
 
matrix_type myHessian
 
LineSearch< function_type, vector_type > myLineSearch
 

Detailed Description

template<class type_>
class goMath::NewtonOpt< type_ >

Newton optimisation.

Todo:
Add line search

This implements the standard Newton step descent algorithm, solving

\[ H(f(x)) \cdot \Delta x = \nabla f(x) \]

to find a step 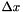$\Delta x$ and then updating

\[ x = x - \Delta x \]

until convergence. A line search is not conducted, this needs to be added.

Parameters
callable_A type that supports the interface defined by the class goMath::OptFunction, with goMath::Matrix and goMath::Vector types as template parameters. You can simply derive from OptFunction and implement the operator() accordingly, or use a OptFunctor. The function to be minimised will be of type callable_.
type_A floating point type (float or double).

Constructor & Destructor Documentation

◆ NewtonOpt()

template<class type_ >
goMath::NewtonOpt< type_ >::NewtonOpt ( goAutoPtr< function_type >  f)
inline

Constructor.

Note
eps is used squared in hessian(), therefore it should not be much smaller than 0.01 for floats in order not to run into machine precision problems.
Parameters
fFunction object that is to be minimised.

Member Function Documentation

◆ setF()

template<class type_ >
void goMath::NewtonOpt< type_ >::setF ( goAutoPtr< function_type >  f)
inline

Sets the function to be minimised.

Parameters
fFunction object that is to be minimised.

◆ solveDirect()

template<class type_ >
virtual void goMath::NewtonOpt< type_ >::solveDirect ( vector_type &  x)
inlinevirtual

Solves without line search.

Parameters
xInitial point.

Reimplemented in goMath::NewtonOptEq< type_ >.

◆ step()

template<class type_ >
virtual void goMath::NewtonOpt< type_ >::step ( vector_type &  x,
vector_type &  ret 
)
inlinevirtual

Calculate the newton step.

Note
x is modified during the call, but restored when the call returns.
Parameters
xPoint at which to calculate
retContains the Newton step on return

Reimplemented in goMath::NewtonOptEq< type_ >.

The documentation for this class was generated from the following file: