Newton optimisation with linear equality constraints. More...
#include <gonewton.h>
Public Types | |
| typedef goMath::Vector< type_ > | vector_type |
| typedef goMath::Matrix< type_ > | matrix_type |
| typedef goMath::OptFunction< matrix_type, vector_type > | function_type |
 Public Types inherited from goMath::NewtonOpt< type_ > Public Types inherited from goMath::NewtonOpt< type_ > | |
| typedef goMath::Vector< type_ > | vector_type |
| typedef goMath::Matrix< type_ > | matrix_type |
| typedef goMath::OptFunction< matrix_type, vector_type > | function_type |
Public Member Functions | |
| NewtonOptEq (goAutoPtr< function_type > f, goAutoPtr< matrix_type > A=0, goAutoPtr< vector_type > b=0) | |
| Constructor. More... | |
| void | setEq (goAutoPtr< matrix_type > A, goAutoPtr< vector_type > b) |
Set the equality constraints 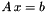 . More... . More... | |
| virtual void | solveDirect (vector_type &x) |
| Solve without line search. More... | |
| virtual void | solveLineSearch (vector_type &x) |
| virtual void | cleanup () |
| Frees temporary memory. | |
| void | initKKT (goSize_t sz) |
| Initialise the KKT system. More... | |
| virtual void | step (vector_type &x, vector_type &ret) |
| Calculate the newton step. More... | |
| void | setInfeasible (bool i) |
| Set infeasibile start point flag. More... | |
| bool | infeasible () const |
| Returns the infeasibile start point flag. More... | |
 Public Member Functions inherited from goMath::NewtonOpt< type_ > Public Member Functions inherited from goMath::NewtonOpt< type_ > | |
| NewtonOpt (goAutoPtr< function_type > f) | |
| Constructor. More... | |
| void | setF (goAutoPtr< function_type > f) |
| Sets the function to be minimised. More... | |
| virtual type_ | newtonDecrement (vector_type &x) |
Protected Attributes | |
| goAutoPtr< matrix_type > | myA |
| goAutoPtr< vector_type > | myB |
| matrix_type | myKKT_A |
| vector_type | myKKT_x |
| vector_type | myKKT_b |
| bool | myInfeasible |
 Protected Attributes inherited from goMath::NewtonOpt< type_ > Protected Attributes inherited from goMath::NewtonOpt< type_ > | |
| goAutoPtr< function_type > | myF |
| matrix_type | myHessian |
| LineSearch< function_type, vector_type > | myLineSearch |
Detailed Description
template<class type_>
class goMath::NewtonOptEq< type_ >
Newton optimisation with linear equality constraints.
- See also
- NewtonOpt
- Todo:
- Detect when Ax=b is fulfilled; then, calculating Ax-b in each step can be skipped (is always feasible then).
- References
- Boyd, S. & Vandenberghe, L.: Convex Optimization. Cambridge University Press, 2004
This is the infeasible start Newton method to solve
![\[ \min f(x) \text{ subject to } A\, x = b \, . \]](../../form_38.png)
The Newton step is here calculated by solving
![\[ \left(\begin{array}{c c} H(F) & A^\top \\ A & 0 \end{array}\right) \cdot \left( \begin{array}{c} \Delta x \\w \end{array} \right) = \left( \begin{array}{c} \nabla F(x) \\A \, x - b \end{array} \right) \]](../../form_39.png)
with H(F) the Hessian matrix of F.
Constructor & Destructor Documentation
◆ NewtonOptEq()
|
inline |
Member Function Documentation
◆ infeasible()
|
inline |
Returns the infeasibile start point flag.
- See also
- setInfeasible()
If true, the initial point may be infeasible.
◆ initKKT()
|
inline |
Initialise the KKT system.
sets the equality constraint matrix A in the matrix
![\[ KKT_A = \left(\begin{array}{c c} H(F) & A^\top \\ A & 0 \end{array}\right) \]](../../form_42.png)
. The hessian H(F) must be filled by the step() method. If necessary, resizes the right hand side vector
![\[ KKT_b \]](../../form_43.png)
of the system
![\[ KKT_A \cdot \left( \begin{array}{c} \Delta x \\w \end{array} \right) = \left( \begin{array}{c} \nabla F(x) \\A \, x - b \end{array} \right) \]](../../form_44.png)
- Parameters
-
sz Dimension of x.
◆ setEq()
|
inline |
◆ setInfeasible()
|
inline |
Set infeasibile start point flag.
- Parameters
-
i If true, the initial point is assumed infeasible.
◆ solveDirect()
|
inlinevirtual |
Solve without line search.
Solves directly without line search. The initial point may be infeasible.
- Parameters
-
x Initial point
Reimplemented from goMath::NewtonOpt< type_ >.
◆ step()
|
inlinevirtual |
Calculate the newton step.
- Note
- x is modified during the call, but restored when the call returns.
- Parameters
-
x Point at which to calculate ret Contains the Newton step on return
Reimplemented from goMath::NewtonOpt< type_ >.
The documentation for this class was generated from the following file:
- gonewton.h
![\[ A \, x = b \, .\]](../../form_40.png)
