goMath::BarrierOptFunctionPhase1< matrix_type, vector_type > Class Template Reference
Public Types | |
| typedef BarrierOptFunction< matrix_type, vector_type > | parent |
| typedef matrix_type::value_type | value_type |
 Public Types inherited from goMath::BarrierOptFunction< matrix_type, vector_type > Public Types inherited from goMath::BarrierOptFunction< matrix_type, vector_type > | |
| typedef OptFunction< matrix_type, vector_type >::value_type | value_type |
| typedef OptFunction< matrix_type, vector_type > | function_type |
 Public Types inherited from goMath::OptFunction< matrix_type, vector_type > Public Types inherited from goMath::OptFunction< matrix_type, vector_type > | |
| typedef vector_type::value_type | value_type |
| Value of the matrix and vector types matrix_type and vector_type. | |
Public Member Functions | |
| BarrierOptFunctionPhase1 (double eps=0.01) | |
| virtual value_type | barrier (const vector_type &x_s) |
Barrier function 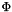 . More... . More... | |
| virtual value_type | operator() (const vector_type &x_s) |
Calculate 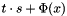 . More... . More... | |
| virtual void | grad (vector_type &x_s, vector_type &ret) |
| Calculate the gradient of f at x. More... | |
| virtual void | hessian (vector_type &x_s, matrix_type &ret) |
| Calculate the Hessian of f at x. More... | |
 Public Member Functions inherited from goMath::BarrierOptFunction< matrix_type, vector_type > Public Member Functions inherited from goMath::BarrierOptFunction< matrix_type, vector_type > | |
| BarrierOptFunction (double eps=0.01) | |
| void | setT (value_type t) |
| value_type | t () const |
| void | setProblem (goAutoPtr< OptProblem< matrix_type, vector_type > > p) |
| virtual void | hessian (vector_type &x, matrix_type &ret) |
| void | barrierGradHessian (const vector_type &x, vector_type &grad, matrix_type &hess) |
| goAutoPtr< OptProblem< matrix_type, vector_type > > | problem () |
Additional Inherited Members | |
 Protected Member Functions inherited from goMath::OptFunction< matrix_type, vector_type > Protected Member Functions inherited from goMath::OptFunction< matrix_type, vector_type > | |
| OptFunction (double eps=0.01) | |
| Constructor. More... | |
 Protected Attributes inherited from goMath::BarrierOptFunction< matrix_type, vector_type > Protected Attributes inherited from goMath::BarrierOptFunction< matrix_type, vector_type > | |
| goAutoPtr< OptProblem< matrix_type, vector_type > > | myProblem |
| vector_type | myBufferGrad |
| matrix_type | myBufferHess |
| value_type | my_t |
Member Function Documentation
◆ barrier()
template<class matrix_type , class vector_type >
|
inlinevirtual |
Barrier function 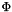 .
.
Calculates the barrier function
![\[ \Phi(x,s) = -\sum_{i=1}^{m} \log (-f_i(x) + s) \]](../../form_7.png)
for all inequality constraints 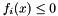 which obviously must be met strictly.
which obviously must be met strictly.
- Parameters
-
x_s Point at which to calculate 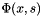 . The last entry of vector
. The last entry of vector x_siss.
Reimplemented from goMath::BarrierOptFunction< matrix_type, vector_type >.
◆ grad()
template<class matrix_type , class vector_type >
|
inlinevirtual |
Calculate the gradient of f at x.
Does a numerical approximation with forward differences. Re-implement for specialisations.
- Note
- x is modified during the call, but restored when the call returns.
- Parameters
-
x Point at which to calculate the gradient ret Contains 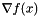 on return
on return
Reimplemented from goMath::BarrierOptFunction< matrix_type, vector_type >.
◆ hessian()
template<class matrix_type , class vector_type >
|
inlinevirtual |
Calculate the Hessian of f at x.
Does a numerical approximation with forward differences. Re-implement for specialisations.
- Note
- x is modified during the call, but restored when the call returns.
- Parameters
-
x Point at which to calculate the Hessian ret Contains 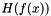 on return
on return
Reimplemented from goMath::OptFunction< matrix_type, vector_type >.
◆ operator()()
template<class matrix_type , class vector_type >
|
inlinevirtual |
Calculate 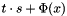 .
.
- See also
- barrier()
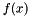 is the original function to be minimised,
is the original function to be minimised, 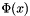 is the log barrier.
is the log barrier.
- Returns
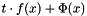
Reimplemented from goMath::BarrierOptFunction< matrix_type, vector_type >.
The documentation for this class was generated from the following file:
- gobarrieropt.h
