An OptFunction that is used in BarrierOpt. More...
#include <gobarrieropt.h>
Public Types | |
| typedef OptFunction< matrix_type, vector_type >::value_type | value_type |
| typedef OptFunction< matrix_type, vector_type > | function_type |
 Public Types inherited from goMath::OptFunction< matrix_type, vector_type > Public Types inherited from goMath::OptFunction< matrix_type, vector_type > | |
| typedef vector_type::value_type | value_type |
| Value of the matrix and vector types matrix_type and vector_type. | |
Public Member Functions | |
| BarrierOptFunction (double eps=0.01) | |
| void | setT (value_type t) |
| value_type | t () const |
| virtual value_type | barrier (const vector_type &x) |
Barrier function 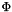 . More... . More... | |
| void | setProblem (goAutoPtr< OptProblem< matrix_type, vector_type > > p) |
| virtual value_type | operator() (const vector_type &x) |
Calculate 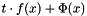 . More... . More... | |
| virtual void | grad (vector_type &x, vector_type &ret) |
| Calculate the gradient of f at x. More... | |
| virtual void | hessian (vector_type &x, matrix_type &ret) |
| void | barrierGradHessian (const vector_type &x, vector_type &grad, matrix_type &hess) |
| goAutoPtr< OptProblem< matrix_type, vector_type > > | problem () |
 Public Member Functions inherited from goMath::OptFunction< matrix_type, vector_type > Public Member Functions inherited from goMath::OptFunction< matrix_type, vector_type > | |
| virtual void | hessian (vector_type &x, matrix_type &ret) |
| Calculate the Hessian of f at x. More... | |
Protected Attributes | |
| goAutoPtr< OptProblem< matrix_type, vector_type > > | myProblem |
| vector_type | myBufferGrad |
| matrix_type | myBufferHess |
| value_type | my_t |
Additional Inherited Members | |
 Protected Member Functions inherited from goMath::OptFunction< matrix_type, vector_type > Protected Member Functions inherited from goMath::OptFunction< matrix_type, vector_type > | |
| OptFunction (double eps=0.01) | |
| Constructor. More... | |
Detailed Description
template<class matrix_type, class vector_type>
class goMath::BarrierOptFunction< matrix_type, vector_type >
An OptFunction that is used in BarrierOpt.
This class provides gradient and Hessian methods for calculating the gradient and Hessian of an optimisation problem set with setProblem() by augmenting the gradient and Hessian of the original objective function by the ones induced by the log barrier function.
The gradient is calculated as ... FIXME
Member Function Documentation
◆ barrier()
|
inlinevirtual |
Barrier function 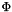 .
.
Calculates the barrier function
![\[ \Phi(x) = -\sum_{i=1}^{m} \log (-f_i(x)) \]](../../form_2.png)
for all inequality constraints 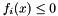 which obviously must be met strictly.
which obviously must be met strictly.
- Parameters
-
x Point at which to calculate 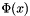 .
.
Reimplemented in goMath::BarrierOptFunctionPhase1< matrix_type, vector_type >.
◆ grad()
|
inlinevirtual |
Calculate the gradient of f at x.
Does a numerical approximation with forward differences. Re-implement for specialisations.
- Note
- x is modified during the call, but restored when the call returns.
- Parameters
-
x Point at which to calculate the gradient ret Contains 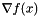 on return
on return
Reimplemented from goMath::OptFunction< matrix_type, vector_type >.
Reimplemented in goMath::BarrierOptFunctionPhase1< matrix_type, vector_type >.
◆ operator()()
|
inlinevirtual |
Calculate 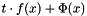 .
.
- See also
- barrier()
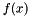 is the original function to be minimised,
is the original function to be minimised, 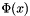 is the log barrier.
is the log barrier.
- Returns
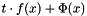
Implements goMath::OptFunction< matrix_type, vector_type >.
Reimplemented in goMath::BarrierOptFunctionPhase1< matrix_type, vector_type >.
The documentation for this class was generated from the following file:
- gobarrieropt.h
