Public Member Functions
virtual bool	run (goFGNode< T, Tfloat > *root, goFactorGraph< T, Tfloat > &fg)
	Run the sum-product algorithm. More...

bool	flooding (goFGNode< T, Tfloat > *startNode, goFactorGraph< T, Tfloat > &fg, goSize_t maxPasses=0)
	"Flooding" type scheme for graphs with loops. More...

bool	variableSend (goFGNode< T, Tfloat > *fgn, goIndex_t parentIndex)
	Create and "send" message from a variable node `fgn` along a given edge. More...

bool	factorSend (goFGNode< T, Tfloat > *fgn, goSize_t parentIndex)
	Create and "send" message from a factor node `fgn` along a given edge. More...

Tfloat	sumproduct (goFGNodeFactor< T, Tfloat > factorNode, goFunctorBase1< Tfloat, const goMath::Vector< T > & > f, goMath::Vector< T > &X, goSize_t i, goSize_t fixed_index)
	Recursive sum/product for the sum-product algorithm. More...

bool	forwardPass (goFGNode< T, Tfloat > *node)

bool	backwardPass (goFGNode< T, Tfloat > *node)

virtual bool	action (goFGNode< T, Tfloat > *node)

bool	marginal (goFGNodeVariable< T, Tfloat > *variable, goSize_t valueCount, goMath::Vector< Tfloat > &marginalRet)

Tfloat	norm (goFactorGraph< T, Tfloat > &fg, goSize_t valueCount)
	Calculate the normalisation constant Z for the given factor graph. More...

Public Member Functions inherited from goMessagePassing< T, Tfloat >
goDouble	sum (goFunctorBase1< Tfloat, const goMath::Vector< T > & > *f, goMath::Vector< T > &X, goSize_t i, goSize_t fixed_index)
	Recursive sum. More...

void	setValueCount (goSize_t c)

goSize_t	getValueCount () const

void	setDirection (Direction d)

Direction	getDirection () const

Public Member Functions inherited from goGraphAlgorithm< goFGNode< T, Tfloat >, goFGEdge< T, Tfloat > >
bool	breadthFirst (goFGNode< T, Tfloat > *root)
	BFS. More...

bool	breadthFirstTree (goFGNode< T, Tfloat > *root)

bool	depthFirstRecursive (goFGNode< T, Tfloat > *root)

bool	depthFirst (goFGNode< T, Tfloat > *root)

bool	depthFirstTree (goFGNode< T, Tfloat > *root)
	Same as depthFirst(), plus fills parent fields in the nodes. More...

virtual bool	action (const goFGNode< T, Tfloat > *node) const

Additional Inherited Members
Public Types inherited from goMessagePassing< T, Tfloat >
enum	Direction { FORWARD, BACKWARD }

Detailed Description

template<class T, class Tfloat>
class goSumProduct< T, Tfloat >

Examples: sumproduct/sp.cpp.

Member Function Documentation

◆ factorSend()

template<class T, class Tfloat>

bool goSumProduct< T, Tfloat >::factorSend	(	goFGNode< T, Tfloat > *	fgn,
		goSize_t	parentIndex
	)

inline

Create and "send" message from a factor node fgn along a given edge.

Parameters

fgn	Factor node to send from.
parentIndex	Index into fgn->adj of edge to send the message along (the other connected node is a variable and "receives" the message).

Returns: True if successful, false otherwise.

◆ flooding()

template<class T, class Tfloat>

bool goSumProduct< T, Tfloat >::flooding	(	goFGNode< T, Tfloat > *	startNode,
		goFactorGraph< T, Tfloat > &	fg,
		goSize_t	maxPasses = `0`
	)

inline

"Flooding" type scheme for graphs with loops.

Uses a sort of flooding message passing schedule (not parallel, but driven by a queue of pending messages).

Parameters

startNode	"Root" node. Does not serve any purpose and may be removed.
fg	Factor graph to work on.
maxPasses	Maximal number of passes each node is allowed to send messages for. If 0 (default), the algorithm will terminate when no more messages are pending. If there are loops in the graph and `maxPasses` is 0, the algorithm will run indefinitely.

Returns: True if successful, false otherwise.

◆ norm()

template<class T , class Tfloat >

Tfloat goSumProduct< T, Tfloat >::norm	(	goFactorGraph< T, Tfloat > &	fg,
		goSize_t	valueCount
	)

inline

Calculate the normalisation constant Z for the given factor graph.

Note: the sum-product algorithm must have run before, so that a marginal can be calculated.

Parameters

fg	Factor graph to calculate the normalisation constant for.
valueCount	Number of possible values for the input to the factors.

Returns: Normalisation constant Z.

◆ run()

template<class T, class Tfloat>

bool goSumProduct< T, Tfloat >::run	(	goFGNode< T, Tfloat > *	root,
		goFactorGraph< T, Tfloat > &	fg
	)

inlinevirtual

Run the sum-product algorithm.

Use setValueCount() to set the values of the variables (they will be in the range [0,valueCount-1]).

Parameters

root	Node to start the algorithm on.
fg	Factor graph to run the algorithm on.

Returns: True if successful, false otherwise.

Implements goMessagePassing< T, Tfloat >.

◆ sumproduct()

template<class T, class Tfloat>

Tfloat goSumProduct< T, Tfloat >::sumproduct	(	goFGNodeFactor< T, Tfloat > *	factorNode,
		goFunctorBase1< Tfloat, const goMath::Vector< T > & > *	f,
		goMath::Vector< T > &	X,
		goSize_t	i,
		goSize_t	fixed_index
	)

inline

Recursive sum/product for the sum-product algorithm.

Calculates 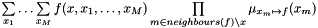$\sum\limits_{x_1} \ldots \sum\limits_{x_M} f(x,x_1,\ldots,x_M) \prod\limits_{m \in neighbours(f)\backslash x} \mu_{x_m \mapsto f}(x_m)$ with x being the variable with fixed_index, $x_1,\ldots,x_M$ the other variables connected to factorNode, and 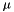$\mu$ the messages stored in the edges between the variable nodes and factorNode. The above term constitutes the messages 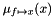$\mu_{f \mapsto x}(x)$ for the sum-product algorithm.

Parameters

factorNode	Factor node to calculate on.
f	Functor of `factorNode` (usually, but can also be a different one).
X	Input for `f`
i	Current index into `X` we are summing over.
fixed_index	Index into `X` of the variable that is held fixed (not summed over).

Returns: The sum/product value.

◆ variableSend()

template<class T, class Tfloat>

bool goSumProduct< T, Tfloat >::variableSend	(	goFGNode< T, Tfloat > *	fgn,
		goIndex_t	parentIndex
	)

inline

Create and "send" message from a variable node fgn along a given edge.

Parameters

fgn	Variable node to send from.
parentIndex	Index into fgn->adj of edge to send the message along (the other connected node is a variable and "receives" the message). Think of it as "outgoingIndex".

Returns: True if successful, false otherwise.

The documentation for this class was generated from the following files:

gosumproduct.h
gosumproduct.cpp

Public Member Functions

Additional Inherited Members

Detailed Description

template<class T, class Tfloat> class goSumProduct< T, Tfloat >

Member Function Documentation

◆ factorSend()

◆ flooding()

◆ norm()

◆ run()

◆ sumproduct()

◆ variableSend()

template<class T, class Tfloat>
class goSumProduct< T, Tfloat >